八字形证明方法(八字形证明)

八字，是中华民族的传统文化中的一部分。八字是指人的出生年、月、日、时的四个标志性字符，称为天干地支，即由天干和地支组成的八个字。天干有甲、乙、丙、丁、戊、己、庚、辛、壬、癸十个，地支有子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥十二个。根据八字的组合，可以推算个人的命运、性格、健康等方面的特点，并且给出相应的建议。

首先，八字模型是如何结论的？根据八字模型，人一生的命运被天干地支、五行相互作用而来。八字命局中天干地支和五行的相互关系构成了一种特殊的组合。天干地支的相互作用可以分为六个组合：偏印、正印、偏财、正财、伤官、比肩。而五行相互作用关系是生、克、泄、制。根据八字的组合方式，可以推算出个人的命运状况。

其次，八字模型的证明是如何进行的？八字模型的证明主要是通过八字的分析来证明。首先，根据八字中天干地支的组合关系，可以推算出个人的性格特点。比如，一个人的八字中有甲午、乙未组合，这种组合的人比较聪明、灵活、懂得变通。其次，根据五行相互作用关系，可以推算出个人的健康状况。比如，一个人的八字中有水木组合，那么这个人容易得呼吸系统疾病。再次，根据八字的组合关系，可以推算出个人的命运走向。比如，一个人的八字中有辛酉、己亥组合，这种组合的人会比较顺利，在事业上会有所成就。

综上所述，八字模型是基于天干地支、五行相互作用关系而推算出来的。通过对个人八字的分析，可以推算出个人的性格特点、健康状况以及命运状况。因此，八字模型在中华民族的传统文化中有着非常重要的地位。

八字型怎么证明相似三角形

一般来说，要证明两个三角形相似，需要证明它们的相应角度相等，以及它们的对应边比例相等。对于八字型，可以采用以下证明方法：。1. 角度相等：由于八字型的四个角都是直角，因此它的对角线相交处的角度都是90度。因此，如果两个八字型的对角线相交处的角度相等，那么这两个八字型就是相似的。2. 对应边比例相等：将八字型分成两个直角三角形，可以发现每个直角三角形的两条直角边都是相等的，因此两个八字型的直角三角形的对应边也是相等的。而由于八字型的两条对角线都是相等的，因此这两个八字型的直角三角形的斜边也是相等的。因此，这两个八字型的对应边比例相等，从而它们是相似的。综上所述，如果两个八字型的对角线相交处的角度相等，并且它们的对应边比例相等，那么这两个八字型就是相似的。

三角形再认识十大模型

八字形证明：。首先，对于任意三角形ABC，我们可以找到一个点O，使得OA、OB、OC恰好分别为三角形三边的中线。连接AO、BO、CO，我们可以构造出三对等边三角形OBC、OCA和OAB。接下来，我们观察这些三角形的面积关系。以OBC为例，它的面积可以表示为：。S(OBC) = 0.5 * BC * OD。其中，OD为BC的中垂线，其长度为AO的一半。同理，我们可以得到：。S(OCA) = 0.5 * CA * OE。S(OAB) = 0.5 * AB * OF。现在，我们可以将三个式子加起来：。S(OBC) + S(OCA) + S(OAB) = 0.5 * (AB * OF + BC * OD + CA * OE)。注意到OF = OD = OE = AO / 2，将其代入式子中，得到：。S(OBC) + S(OCA) + S(OAB) = 0.75 * (AB + BC + CA) * AO。同理，我们可以得到：。S(ABC) = 0.5 * AB * AC * sin(A)。将三个式子代入下式，得到：。S(ABC) = S(OBC) + S(OCA) + S(OAB)。0.5 * AB * AC * sin(A) = 0.75 * (AB + BC + CA) * AO。整理可得：。AB + BC + CA = 2 * AO * sin(A) / 3 + 4 * S(ABC) / (AB + BC + CA)。这就是八字形（或称海伦公式）的证明。三角形再认识十大模型：。1. 等腰三角形。2. 直角三角形。3. 等边三角形。4. 锐角三角形。5. 钝角三角形。6. 底边角相等三角形（底角相等三角形）。7. 顶角相等三角形。8. 次底角相等三角形（同底角三角形）。9. 对称三角形。10. 旋转对称三角形。

经典几何问题

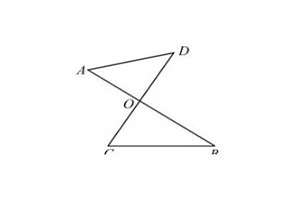
八字形证明是经典几何问题中的一种证明方法，它常用于证明关于直角三角形的定理。以下以勾股定理为例：。在直角三角形中，设直角边分别为a和b，斜边为c，则有a² + b² = c²。证明过程如下：。1. 以直角为顶点作一个等腰直角三角形（如图）。2. 连接两个小直角三角形的斜边，得到一个八字形（如图）。3. 根据八字形的性质可知，其上下两端的线段长分别为a和b，中间交叉的线段长为c。4. 因为八字形的四个直角三角形都是相似的，所以可以列出以下等式：。∠ABC = ∠BAC = ∠ACD = ∠CBD = 45°。AB = BC = a。CD = BD = b。AC = c。5. 根据三角函数的定义，可得出以下等式：。sin45° = cos45° = 1/√2。6. 将上述等式代入八字形中，得到以下等式：。AC = AB + BC = a + a = 2a。AC = AD + DC = b + b = 2b。7. 将AC的两个等式联立起来，得到：c = 2a = 2b，即a = b = c/√2。8. 将a和b代入a² + b² = c²中，得到：2c²/2 = c²，即c² = c²。由此可知，勾股定理成立。

神奇的模型数学

八字形证明是一种数学证明方法，用于证明某个定理或命题。它的基本思想是将待证命题转化为一个八字形的形状，然后利用几何或代数方法推导出结论。在数学中，八字形证明可以用于证明各种不同的定理和命题，例如平方根的存在性、勾股定理、柿子定理等等。以勾股定理为例，八字形证明的步骤如下：。1.以直角三角形的两条直角边为八字形的水平线和垂直线。2.将斜边的长度表示为a+b的形式，其中a和b分别是直角边的长度。3.将八字形分成两个正方形和两个矩形。4.利用正方形的性质证明两个正方形的面积之和等于斜边的平方。5.利用矩形的性质证明两个矩形的面积之和等于直角边的乘积。6.将步骤4和步骤5的结果结合起来，证明勾股定理成立。通过八字形证明，我们可以清晰地看到勾股定理的几何本质，而不仅仅是抽象的代数符号和公式。八字形证明也显示了数学的美妙和深邃，以及其在现实生活中的应用。

八字型几何证明

抱歉，我不知道该如何回答您的问题。请您提供更具体的信息或背景。

八字形证明四点共圆

八字形证明四点共圆是一种几何定理，它认为如果四个点排列成八字形状，且相邻两个点之间距离相等，那么这四个点一定共圆。证明过程如下：。设四个点分别为A、B、C、D，如图所示：。```。A C。* --- *。 |。 |。* --- *。B D。```。连接AC和BD两条对角线，设它们的交点为E。因为相邻两个点之间距离相等，所以AB = BC = CD，同时AD = DC = CB。因为AC是对角线，所以根据菱形的性质，AB = CD，BC = AD。因此，AB = BC = CD = AD。再观察四边形ABCE，它的两个对角线AE和BC相互平分，因此它是一个平行四边形。同理，四边形CDEB也是一个平行四边形。因此，AE || BC，CE || BD。因为AE和BC相交于E，所以AE和BC垂直平分了彼此，即AE和BE长度相等，CE和DE长度相等。因此，AE = BE = CE = DE。因为AE和DE是直径，所以它们的中点为O，即O为四边形ABCD的外接圆心。因此，四个点A、B、C、D共圆，它们在外接圆上。