八字形定理证明过程(八字形定理)

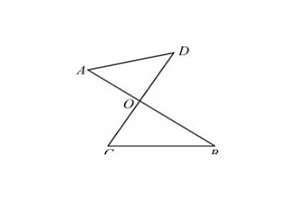
八字形定理是初中数学中的一个重要定理，它不仅可以用于解决几何题目，还可以在其它数学学科中发挥作用。初中常见的几何模型有很多，包括三角形、矩形、平行四边形、梯形等等。下面我们将以八字形定理为主线，探究这些几何模型的一些性质和应用。

一、三角形。

三角形是初中数学中最基本的几何图形之一，也是最常见的几何模型之一。在三角形中，八字形定理可以用于解决很多关于直角三角形的问题，例如，如果一个直角三角形的两条直角边分别为3厘米和4厘米，那么斜边的长度是多少？根据八字形定理，我们可以得出：$3^2+4^2=c^2$，解得$c=5$。因此，这个直角三角形的斜边长为5厘米。

二、矩形。

矩形是初中数学中另一个很常见的几何模型，它有很多重要性质。通过八字形定理，我们可以得到矩形中两条对角线的关系。设矩形的长为a，宽为b，则矩形的对角线的长度为$\sqrt{a^2+b^2}$。这个结论可以通过将矩形对角线分成两条相交的直线段，然后利用勾股定理证明得到。

三、平行四边形。

平行四边形是初中数学中比较复杂的几何模型之一，但它有一些很重要的性质。通过八字形定理，我们可以得到平行四边形中对角线的关系。设平行四边形的相邻两边分别为a和b，对角线的长度为c，则有：$a^2+b^2=c^2+d^2$，其中d是平行四边形的另一条对角线的长度。这个结论可以通过将平行四边形对角线分成两条相交的直线段，然后利用勾股定理证明得到。

四、梯形。

梯形是初中数学中比较难解决的几何模型之一，但它也有一些重要的性质。通过八字形定理，我们可以得到梯形的一些关系。设梯形的上底为a，下底为b，高为h，斜边为c，则有：$c^2=h^2+(b-a)^2$。这个结论可以通过将梯形分成两个直角三角形，然后利用勾股定理证明得到。

总之，八字形定理是初中数学中一个非常重要的定理，它可以解决很多与几何图形相关的问题。通过应用八字形定理，我们可以更好地理解各种几何模型的性质和应用，从而更好地掌握初中数学中与几何相关的知识。

八字命理中的二八定律

八字形定理和八字命理中的二八定律是两个不同的概念。八字形定理指的是八字命盘中五行的相生相克关系，即“一生水，二生木，三生火，四生土，五生金”，以及相应的克制关系，“水克火，火克金，金克木，木克土，土克水”。这个定理是八字命理中非常基础的概念，也是其他命理理论的基础。而八字命理中的二八定律则是指每个人在命理中有一个“二八运势”或“二八格局”。具体来说，就是说每个人一生中的运势会在20岁和60岁左右有一个转折点，这两个点之前和之后的运势会有较大的差别。因此，有人说“二八定律”是指一个人一生中80%的成就都会在20岁到60岁之间实现。这个说法并没有科学依据，只是一种流行的迷信而已。

8字模型与飞镖模型

八字形定理、8字模型和飞镖模型都是基于数学的理论模型，但它们应用于不同的领域。八字形定理是一种概率统计学的工具，用来估计在样本容量充分大的情况下，样本均值与总体均值之间的差异。它得名于将样本容量、样本平均值、总体平均值和样本标准差分别标记为“八字形”。8字模型是一种管理学的工具，用于描述组织或企业的八种不同属性，包括战略、结构、系统、文化、人员、技术、任务和环境。这些属性是相互关联且相互影响的，通过使用8字模型可以帮助企业更好地理解和优化自身的运营。飞镖模型是一种市场营销学的工具，用于描述在市场中如何开发和发行新产品。它包括四个步骤：理解市场、确定目标市场、设计产品和开发营销计划。飞镖模型得名于其形状类似于飞行中的飞镖，其中市场洞察是飞镖的头部，而其余三个步骤则组成了飞镖的身体部分。

经典几何问题

八字形定理是一个经典的几何定理，也被称为垂心定理或高线定理。它指出，在一个三角形中，垂足连成的四边形是一个八字形，其对角线相交于三角形的垂心。垂足即从三角形的一个顶点向对边的垂线与对边的交点。这个定理对于解决一些三角形的性质以及构造中有重要应用。八字形定理的证明可以通过类似于勾股定理的方式进行，具体来说，如果将一条垂线从三角形的顶点向对边作垂线，则可以将三角形分成两个直角三角形和一个相似三角形。在这个过程中，垂足与对应的角的大小是相关的，特别的，在垂足所在的直线即高线上的任何一点，只要是在垂线所在的直线上，其所在的四边形都是八字形，相互之间是全等的。因此，垂足所在的直线在三角形的性质中起着重要的作用。

神奇的模型数学

八字形定理是一种神奇的模型数学，它能够将一些看似不相关的数学概念联系起来，并给出一种简单而富有洞见的解释。该定理的基础在于，每一个正整数都可以用四种不同的数学运算符号（加号、减号、乘号、除号）和三个左右括号组合而成，且这些运算符号和括号的组合方式可以用八个不同的字符来表示，如下图所示：。![八字形定理示意图]()。于是，我们可以将任何一个正整数表示为一个八字形字符串，例如：。- 24 = (1+2)×(3+4)。- 7 = (1+2)×3-4。- 100 = (1+2+3+4)×(5-6)+7×8+9。然后，我们可以使用一些数学方法来研究这些八字形字符串，比如计算它们的长度、求出它们的因数个数等等，从而得到一些有趣的结论。例如，以下两个结论是基于八字形定理的：。- 每个八字形字符串的长度都是偶数。- 对于任何一个正整数，它的因数个数与其八字形字符串的长度呈正相关关系。八字形定理的应用领域非常广泛，涉及到数学、计算机科学、物理学等多个领域。它不仅具有高度的理论意义，还可以用于设计和优化算法、解决一些实际问题等等。

三角形基础之十大模型

八字形定理：。在一个八字形中，如果一对对角线互相垂直，那么对角线上的四个点连成的四条线段必定相等。十大三角形基础模型：。1. 直角三角形。一个角为直角（即90度），另两个角分别为锐角和钝角，对直角的两条边称为直角边，直角边所对的角称为对角。2. 等腰三角形。至少两条边相等，又称为等腰锐角三角形、等腰钝角三角形、等腰直角三角形。等腰三角形的高是从底边延长至对角上的垂线，底边中心线是两底边中心的连线。3. 等边三角形。三条边都相等，对于等边三角形，三个内角都是60度。它的高和中心线都是重合的，且三角形的高、中线和中位线重合。4. 一般三角形。对于任意的三边形，都可以将它划分为一些小三角形进行计算。5. 直线三角形。三角形的一条边与一条直线相交，构成的三角形称为直线三角形。6. 旁切圆三角形。三角形的内切圆切于三角形的一边上，对应这条边的两个切点与圆心组成的三角形称为旁切圆三角形。7. 海伦公式三角形。利用海伦公式求解面积的三角形。8. 正弦定理三角形。利用正弦定理求解三角形。9. 余弦定理三角形。利用余弦定理求解三角形。10. 外接圆三角形。三角形三个顶点在同一个圆上，称为外接圆三角形。它们的外心是外切圆的圆心。